什么是置信区间?
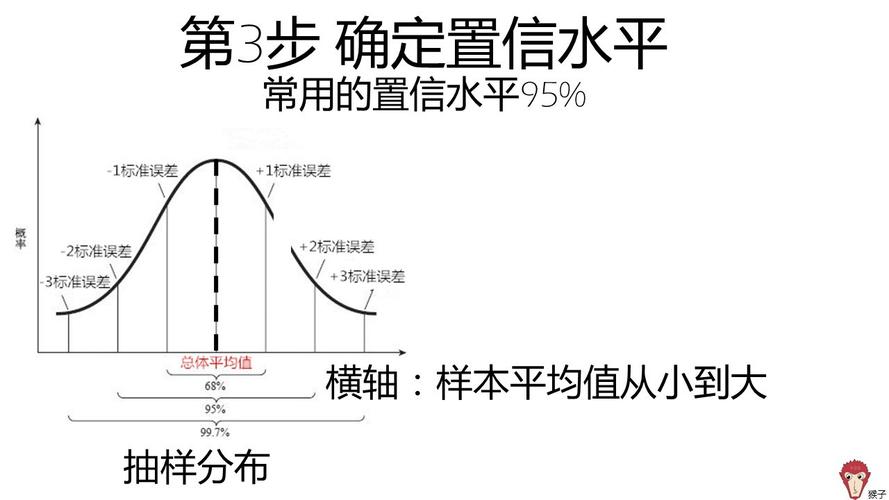
置信区间是指在一定的置信水平下,总体参数的可能取值范围。通常,我们使用样本数据来估计总体参数,但由于样本的随机性,估计值会存在一定的不确定性。置信区间就是用来描述这种不确定性的区间估计方法。,如果我们说某个总体均值的95%置信区间是[
50, 60],这意味着在95%的置信水平下,总体均值有95%的概率落在这个区间内。
如何计算置信区间?
计算置信区间的基本步骤
计算置信区间通常需要以下几个步骤:确定样本数据的均值和标准差;根据样本大小和置信水平,查找相应的临界值(如t值或z值);利用公式计算置信区间的上下限。具体公式如下:
对于正态分布的总体,置信区间的计算公式为:
置信区间 = 样本均值 ± (临界值 × 标准误差)
其中,标准误差 = 标准差 / √样本大小。
不同置信水平的选择
置信水平是表示我们对置信区间的信心程度,常见的置信水平有90%、95%和99%。置信水平越高,置信区间越宽,表示我们对总体参数的估计越不确定。在实际应用中,通常选择95%的置信水平,以在准确性和不确定性之间取得平衡。
置信区间的应用场景
置信区间在统计学和数据分析中有着广泛的应用。以下是一些常见的应用场景:
常见问题与解答
问题1:置信区间和置信水平有什么区别?
置信区间是总体参数的可能取值范围,而置信水平是表示我们对这个区间的信心程度。,95%的置信水平意味着在100次抽样中,有95次置信区间会包含总体参数。
问题2:置信区间越宽越好还是越窄越好?
置信区间的宽度反映了估计的精确性。置信区间越窄,表示估计越精确;置信区间越宽,表示估计越不确定。在实际应用中,我们希望在一定的置信水平下,置信区间尽可能窄,以提高估计的精确性。
问题3:如何选择合适的置信水平?
选择合适的置信水平需要根据具体的研究目的和需求。通常,95%的置信水平是一个常用的选择,因为它可以在准确性和不确定性之间取得平衡。如果对估计的精确性要求较高,可以选择更高的置信水平,如99%。
置信区间是统计学中一个重要的工具,用于估计总体参数的可能范围。通过理解置信区间的定义、计算方法和应用场景,我们可以更好地进行数据分析和决策。希望本文能够帮助读者全面掌握置信区间的相关知识,并在实际应用中灵活运用。


