滑动窗口的基本原理
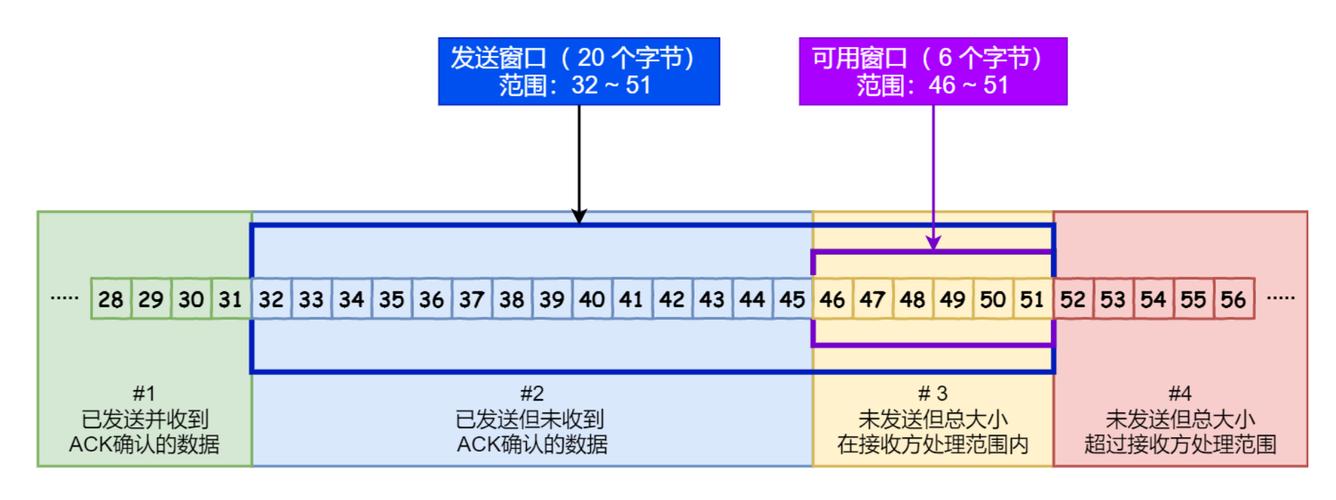
滑动窗口算法的核心思想是通过维护一个窗口来跟踪数组或字符串中的连续元素。这个窗口可以是一个固定大小,也可以根据特定条件动态调整。窗口通常由两个指针表示:左指针(left)和右指针(right),它们分别表示窗口的起始和结束位置。
固定大小窗口
固定大小的滑动窗口是最简单的形式,窗口大小在算法执行过程中保持不变。这种类型的滑动窗口常用于解决需要计算固定长度子序列的问题,如计算数组中所有长度为k的子数组的平均值。
可变大小窗口
可变大小的滑动窗口更为灵活,窗口大小会根据特定条件动态调整。这类窗口常用于解决需要找到满足特定条件的最长子序列或最短子序列的问题,如在字符串中查找包含所有指定字符的最短子串。
滑动窗口的实现方法
实现滑动窗口算法通常需要以下几个关键步骤:初始化窗口指针、扩展窗口、收缩窗口以及更新结果。下面我们通过一个具体例子来说明这些步骤。
初始化阶段
需要初始化窗口的左右指针,通常将它们都设置为0。同时可能需要初始化一些辅助变量,如哈希表用于记录窗口内元素的频率,或者变量用于记录当前窗口的状态。
窗口扩展阶段
右指针逐步向右移动,扩展窗口的大小。在每次扩展时,需要更新窗口的状态,如将新元素加入哈希表,或者更新当前窗口的统计信息。
窗口收缩阶段
当窗口满足特定条件时(如包含所有目标字符),左指针开始向右移动,收缩窗口。收缩过程中同样需要更新窗口状态,并检查是否仍然满足条件。
结果更新阶段
在窗口扩展和收缩的过程中,需要不断检查当前窗口是否满足问题的要求,并在满足时更新最终结果。,记录满足条件的最小窗口大小或最长子序列长度。
滑动窗口的典型应用场景
滑动窗口算法在解决各种字符串和数组问题时表现出色,下面介绍几个典型的应用场景。
字符串匹配问题
滑动窗口非常适合解决字符串匹配问题,如查找字符串中所有字母异位词、最小覆盖子串等。这类问题通常需要跟踪窗口内字符的频率,并与目标字符串的字符频率进行比较。
数组子序列问题
在数组中查找满足特定条件的子序列也是滑动窗口的常见应用,如最大连续1的个数、和为k的最长子数组等。这些问题通常需要维护窗口内元素的某种统计信息。
数据流处理
滑动窗口还可用于处理数据流中的问题,如计算滑动窗口平均值、滑动窗口最大值等。这类问题通常需要结合队列或双端队列来实现高效的窗口维护。
滑动窗口的优化技巧
虽然滑动窗口算法已经很高效,但在某些情况下还可以进一步优化。下面介绍几种常见的优化方法。
滑动窗口是一种强大而灵活的算法技巧,掌握它可以有效解决许多常见的编程问题。通过理解其基本原理、熟悉实现方法并了解各种应用场景,读者可以在实际编程中灵活运用这一技术,提高算法效率和代码质量。
常见问题解答
1. 滑动窗口和双指针算法有什么区别?
滑动窗口实际上是双指针算法的一种特殊形式。双指针算法更通用,两个指针可以以不同方式移动;而滑动窗口特指维护一个连续子序列的窗口,通常用于解决子串、子数组问题。
2. 如何判断一个问题是否适合用滑动窗口解决?
如果问题涉及数组或字符串的连续子序列,并且可以通过维护一个窗口来逐步求解,那么很可能适合使用滑动窗口。典型特征包括:需要计算子序列的和、平均值,或者查找满足特定条件的最短/最长连续子序列。
3. 滑动窗口算法的时间复杂度通常是多少?
滑动窗口算法通常可以将时间复杂度优化到O(n),因为每个元素最多被左指针和右指针各访问一次。这是相比暴力解法O(n²)的巨大改进。
4. 滑动窗口算法在实际工程中有哪些应用?
滑动窗口在实际工程中有广泛应用,如网络流量控制中的拥塞窗口、实时数据处理中的时间窗口统计、用户行为分析中的会话窗口等。理解这一算法有助于解决各种实际工程问题。


